Tree (set theory)

In set theory, a tree is a partially ordered set (poset) (T, <) such that for each t ∈ T, the set {s ∈ T : s < t} is well-ordered by the relation <. For each t ∈ T, the order type of {s ∈ T : s < t} is called the height of t (denoted ht(t, T)). The height of T itself is the least ordinal greater than the height of each element of T. A root of a tree T is an element of height 0. Frequently trees are assumed to have only one root (as the typical questions that are investigated in this field are easily reduced to questions about single-rooted trees).

Trees with a single root in which each element has finite height can be naturally viewed as rooted trees in the graph-theoretical sense: there is an edge from x to y if and only if y is a direct successor of x (i.e., x<y, but there is no element between x and y). However, if T is a tree of height > ω, then there is no natural edge relation that will make T a tree in the sense of graph theory.

A branch of a tree is a maximal chain in the tree (that is, any two elements of the branch are comparable, and any element of the tree not in the branch is incomparable with at least one element of the branch). The length of a branch is the ordinal that is order isomorphic to the branch. A tree is a κ-tree if and only if it has height κ and every level has size less than κ. For each ordinal α, the α-th level of T is the set of all elements of T of height α. The width of a tree is the supremum of the cardinalities of its levels.

There are some fairly simply stated yet hard problems in infinite tree theory. Examples of this are the Kurepa conjecture and the Suslin conjecture. Both of these problems are known to be independent of Zermelo-Fraenkel set theory. König's lemma states that every ω-tree has an infinite branch. On the other hand, it is a theorem of ZFC that there are uncountable trees with no uncountable branches and no uncountable levels; such trees are known as Aronszajn trees. A κ-Suslin tree is a tree of height κ which has no chains or antichains of size κ. In particular, if κ is singular (i.e. not regular) then there exists a κ-Aronszajn tree and a κ-Suslin tree. In fact, for any infinite cardinal κ, every κ-Suslin tree is a κ-Aronszajn tree (the converse does not hold).

Note: the Suslin conjecture was originally stated as a question about certain total orderings but it is equivalent to the statement: Every tree of height ω₁ has an antichain of cardinality ω₁ or a branch of length ω₁.

1 Tree (automata theory)
- 1.1 Example
2 See also
3 External links
4 References

Tree (automata theory)

Following definition of the tree is slightly different formalism of the tree compare to above introduction. For example, each node of the tree is a word over set of natural numbers(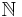 $\mathbb{N}$ ), which helps this definition to be used in automata theory.

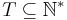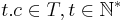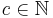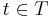A tree is a set $T \subseteq \mathbb{N}^{*}$ such that if $t.c \in T, t \in \mathbb{N}^{*}$ and $c \in \mathbb{N}$ then, $t \in T$ and for all 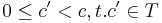$0 \leq c' < c, t.c' \in T$ . The element of $T$ are known as nodes and empty word $\epsilon$ is root of $T$ . For every 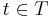$t \in T$ , the element 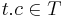$t.c \in T$ is a successor of $t$ in direction $c$ . The number of successors of $t$ is called the degree or arity of $t$ and represented as $d(t)$ . 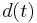A node is a leaf if it has no successors. If every node of a tree has finitely many successors then it is finitely branching tree, otherwise infinitely branching tree. 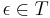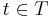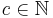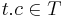A path $\pi$ is a subset of $T$ such that $\epsilon \in T$ and for every $t \in T$ , either $t$ is a leaf or there exist a unique $c \in \mathbb{N}$ such that $t.c \in T$ . A path may be a finite or infinite set. If all paths of a tree are finite then tree is called finite, otherwise infinite. A tree is called fully infinite if all paths of the tree are infinite. 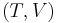Given an alphabet $\Sigma$ , a $\Sigma$ -labeled tree is a pair $(T,V )$ , where T is a tree and 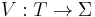$V: T \rightarrow \Sigma$ maps each node of $T$ to a letter in $\Sigma$ . A labeled tree formally defines commonly used term tree structure. A set of labeled trees is called a tree language.

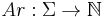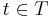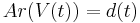A tree is ranked if there is an order among successors of each node of the tree. Above definition of tree naturally suggest an order among successors, which can be used to make tree ranked. Sometimes, an extra function $Ar: \Sigma \rightarrow \mathbb{N}$ is defined. This function associate a fixed arity to each letter of alphabet. In this case for each $t \in T$ has to satisfy $Ar(V(t))=d(t)$ .

For example, above definition is used in defining infinite tree automaton.

Example

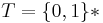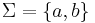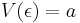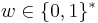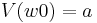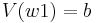Let $T = \{0,1\}*$ and $\Sigma = \{a,b\}$ . We define labeling function V as follows, labeling for root node is $V(\epsilon) = a$ and, for every other node $w \in \{0,1\}^{*}$ , the labellings for successor nodes are $V(w0) = a$ and $V(w1) = b$ . It is clear from the picture that T forms infinite(full) binary tree.

External links

Sets, Models and Proofs by Ieke Moerdijk and Jaap van Oosten, see Definition 3.1 and Exercise 56 on pp. 68–69.
tree (set theoretic) by Henry on PlanetMath
branch by Henry on PlanetMath
example of tree (set theoretic) by uzeromay on PlanetMath

References

Jech, Thomas (2002). Set Theory. Springer-Verlag. ISBN 3-540-44085-2.
Kunen, Kenneth (1980). Set Theory: An Introduction to Independence Proofs. North-Holland. ISBN 0-444-85401-0. Chapter 2, Section 5.
Monk, J. Donald (1976). Mathematical Logic. New York: Springer-Verlag. pp. 517. ISBN 0-387-90170-1.
Hajnal, András; Hamburger Péter (1999). Set Theory. Cambridge: Cambridge University Press.

Tree (set theory)

Contents

Tree (automata theory)

Example

See also

External links

References